最优传输理论：重塑概率分布度量，驱动AI前沿应用

## 核心洞察与关键发现

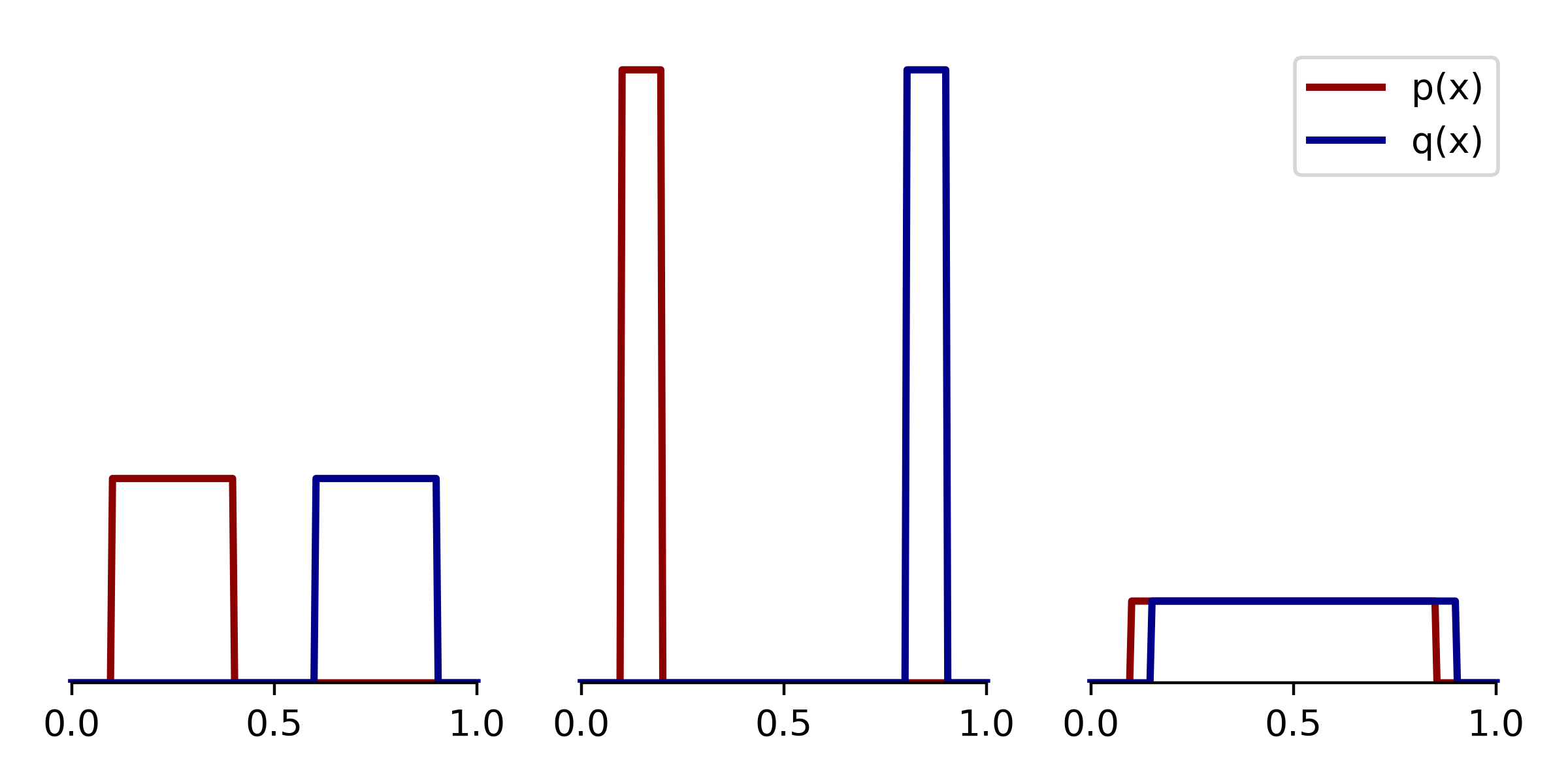
最优传输理论及其核心的 Wasserstein 距离（又称“土方距离”）为衡量概率分布间的“距离”提供了强大而直观的框架。与 Kullback-Lieibler (KL) 散度等方法相比，Wasserstein 距离在处理支持集不重叠的分布时，能提供有限且符合直觉的度量，并天然满足距离的对称性和三角不等式。该理论通过一个“搬运”思想实验得以具象化：将一份概率分布（如泥土堆）以最小化总运输成本（通常为距离的平方）的方式，匹配到另一份概率分布（如需要填平的坑洞）。其核心在于寻找一个最优的运输计划（Transport Plan），即确定如何将源分布的质量转移到目标分布的各个位置。

## 战略分析与趋势预判

最优传输理论的应用正迅速扩展至图像处理、生成模型（如 GANs）和生物数据分析等前沿领域。其将衡量概率分布间差异的问题转化为一个可求解的线性规划问题，使得在离散化场景下，可以通过标准算法（如单纯形法）有效求解。近期，通过引入熵正则化，显著提升了算法在高维数据上的计算效率，为大规模机器学习和数据科学应用打开了更广阔的空间。该理论不仅为量化分布差异提供了更鲁棒的工具，也为理解和构建生成模型提供了新的视角。

A Short Introduction to Optimal Transport and Wasserstein Distance · Its Neuronal